Analisis Kinerja Algoritma Genetika pada Persoalan NP-Complete
Analisis Kinerja Algoritma Genetika pada Persoalan NP-Complete – Bayangin kamu punya masalah yang super rumit, kayak nyusun puzzle yang bagiannya banyak banget dan gak ada petunjuk. Masalah ini bisa dipecahkan, tapi butuh waktu lama banget, bahkan komputer super canggih pun kewalahan. Nah, di sinilah Algoritma Genetika muncul sebagai pahlawan! Algoritma ini terinspirasi dari evolusi alam, dengan prinsip ‘survival of the fittest’ yang membantu kita menemukan solusi optimal untuk masalah-masalah rumit, termasuk masalah NP-Complete yang super sulit.
Analisis Kinerja Algoritma Genetika pada Persoalan NP-Complete adalah topik yang seru banget, karena membahas kemampuan Algoritma Genetika dalam menghadapi masalah-masalah yang super sulit dipecahkan. Di sini, kita akan menjelajahi cara kerja Algoritma Genetika, memahami karakteristik masalah NP-Complete, dan melihat bagaimana Algoritma Genetika bisa memberikan solusi yang efisien untuk masalah-masalah tersebut.
Analisis Kinerja Algoritma Genetika pada Persoalan NP-Complete

Dalam dunia komputasi, kita seringkali berhadapan dengan masalah yang rumit dan membutuhkan waktu komputasi yang sangat lama untuk menemukan solusi optimal. Masalah-masalah ini dikenal sebagai masalah NP-Complete, yang artinya solusi untuk masalah tersebut sulit ditemukan dalam waktu polinomial. Salah satu pendekatan yang menarik untuk menyelesaikan masalah NP-Complete adalah dengan menggunakan Algoritma Genetika (AG).
Algoritma Genetika terinspirasi dari proses evolusi biologis, di mana individu-individu yang lebih kuat dan lebih adaptif bertahan hidup dan mewariskan sifat-sifatnya kepada generasi berikutnya. AG bekerja dengan menciptakan populasi solusi potensial dan melakukan operasi genetika seperti seleksi, crossover, dan mutasi untuk menghasilkan solusi yang lebih baik secara bertahap.
Proses ini berulang hingga mencapai solusi yang memuaskan.
Contoh Masalah NP-Complete
Banyak masalah dalam kehidupan nyata dikategorikan sebagai NP-Complete. Berikut adalah beberapa contoh yang umum dijumpai:
- Travelling Salesman Problem (TSP):Mencari rute terpendek yang mengunjungi setiap kota tepat sekali dan kembali ke kota awal.
- Knapsack Problem:Menentukan barang-barang yang dapat dimasukkan ke dalam ransel dengan kapasitas terbatas, sehingga nilai total barang yang dimasukkan maksimal.
- Graph Coloring Problem:Menentukan warna untuk setiap simpul dalam graf, sehingga tidak ada dua simpul yang bertetangga memiliki warna yang sama.
Tujuan Analisis Kinerja Algoritma Genetika pada Masalah NP-Complete
Tujuan utama dari analisis kinerja Algoritma Genetika pada masalah NP-Complete adalah untuk memahami:
- Efektivitas AG dalam menemukan solusi yang baik:Apakah AG mampu menghasilkan solusi yang mendekati optimal dalam waktu yang relatif singkat?
- Ketergantungan kinerja AG terhadap parameter-parameternya:Bagaimana perubahan parameter seperti ukuran populasi, probabilitas crossover, dan probabilitas mutasi memengaruhi kinerja AG?
- Perbandingan kinerja AG dengan algoritma lain:Bagaimana kinerja AG dibandingkan dengan algoritma lain yang digunakan untuk menyelesaikan masalah NP-Complete?
Konsep Algoritma Genetika
Algoritma Genetika (AG) adalah teknik komputasi yang terinspirasi dari proses evolusi biologis. AG digunakan untuk memecahkan masalah optimasi dengan meniru mekanisme seleksi alam dan genetika.
Prinsip Dasar Algoritma Genetika
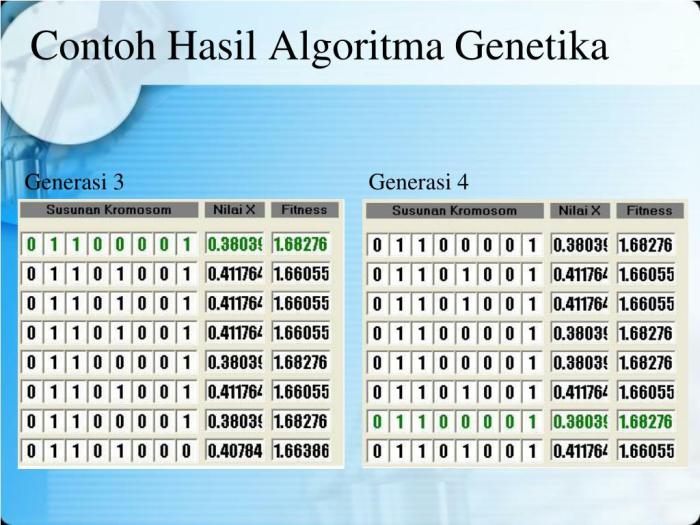
AG bekerja dengan menciptakan populasi solusi potensial yang direpresentasikan sebagai kromosom (string yang berisi informasi genetik). Kromosom ini berevolusi melalui serangkaian iterasi yang disebut generasi, dengan setiap generasi terdiri dari beberapa langkah utama.
Langkah-Langkah Utama Algoritma Genetika
Langkah-langkah utama dalam AG meliputi:
- Inisialisasi Populasi:Menciptakan populasi awal kromosom secara acak.
- Evaluasi Kebugaran:Menentukan nilai kebugaran setiap kromosom berdasarkan fungsi objektif masalah.
- Seleksi:Memilih kromosom dengan kebugaran tinggi untuk berkembang biak.
- Crossover:Menggabungkan materi genetik dari dua kromosom terpilih untuk menciptakan kromosom baru.
- Mutasi:Mengubah secara acak beberapa gen dalam kromosom untuk memperkenalkan variasi.
- Generasi Baru:Mengulang langkah seleksi, crossover, dan mutasi untuk menghasilkan generasi kromosom baru.
Peran Operator Genetika
Operator genetika berperan penting dalam proses evolusi AG:
- Crossover:Menggabungkan materi genetik dari dua kromosom terpilih, menghasilkan kromosom baru yang mewarisi sifat-sifat baik dari kedua orang tuanya. Proses ini memungkinkan eksplorasi ruang solusi yang lebih luas.
- Mutasi:Mengubah secara acak beberapa gen dalam kromosom, memperkenalkan variasi baru ke dalam populasi. Mutasi membantu menghindari solusi lokal optimal dan mengeksplorasi area solusi yang belum dijelajahi.
- Seleksi:Memilih kromosom dengan kebugaran tinggi untuk berkembang biak, memastikan bahwa kromosom dengan solusi yang lebih baik diwariskan ke generasi berikutnya. Seleksi mendorong evolusi menuju solusi yang lebih optimal.
Contoh Penerapan Algoritma Genetika
AG telah diterapkan secara luas dalam berbagai bidang, termasuk:
- Optimasi Desain:Mencari desain optimal untuk produk, struktur, atau proses. Contohnya, AG dapat digunakan untuk mengoptimalkan desain sayap pesawat terbang atau mendesain sirkuit elektronik.
- Perencanaan dan Penjadwalan:Mencari jadwal atau rencana optimal untuk berbagai aktivitas. Contohnya, AG dapat digunakan untuk menjadwalkan produksi di pabrik atau merencanakan rute pengiriman.
- Pengenalan Pola:Mengidentifikasi pola atau tren dalam data. Contohnya, AG dapat digunakan untuk mengidentifikasi pola dalam data medis untuk diagnosis penyakit atau menganalisis data pasar keuangan.
Masalah NP-Complete
Bayangin kamu punya tugas yang super duper ribet, kayak nyusun puzzle yang jumlahnya udah nggak kehitung, atau nyari kunci yang pas buat buka brankas super canggih. Nah, masalah-masalah kayak gitu yang punya tingkat kesulitan tinggi, bahkan buat komputer super canggih, disebut sebagai masalah NP-Complete.
Definisi Masalah NP-Complete
Masalah NP-Complete adalah masalah yang termasuk dalam kelas kompleksitas NP (Non-deterministic Polynomial Time), dan punya sifat unik yang membuatnya sulit dipecahkan secara efisien. Sederhananya, masalah NP-Complete adalah masalah yang butuh waktu lama banget buat dicari solusinya, bahkan buat komputer super canggih.
Karakteristik Masalah NP-Complete
Masalah NP-Complete punya beberapa ciri khas yang membuatnya sulit ditaklukkan:
- Verifikasi solusi mudah:Kalau kamu udah nemuin solusi buat masalah NP-Complete, gampang banget buat ngecek apakah solusi itu benar atau salah.
- Mencari solusi sulit:Masalahnya, buat nemuin solusi itu sendiri, butuh waktu yang super lama. Semakin kompleks masalahnya, semakin lama waktu yang dibutuhkan buat nyari solusinya.
- Tidak ada algoritma efisien:Sampai saat ini, belum ada algoritma yang bisa menyelesaikan masalah NP-Complete secara efisien dalam waktu polynomial. Algoritma yang ada biasanya butuh waktu eksponensial, yang artinya semakin besar masalahnya, semakin lama waktu yang dibutuhkan buat menyelesaikannya.
Contoh Masalah NP-Complete
Ada banyak masalah NP-Complete di dunia nyata, nih, contohnya:
- Traveling Salesman Problem (TSP):Masalah ini tentang nyari rute terpendek buat mengunjungi semua kota dalam suatu wilayah, tanpa harus mengunjungi kota yang sama dua kali. Bayangin kamu mau keliling Indonesia, tapi mau nyari rute yang paling efisien buat ngehemat waktu dan bensin. Nah, itu contoh masalah TSP.
- Knapsack Problem:Bayangin kamu lagi liburan dan mau ngisi tas ransel dengan barang-barang yang kamu butuhkan. Tapi, tas kamu punya kapasitas terbatas. Nah, masalah ini tentang nyari kombinasi barang yang paling optimal buat masuk ke dalam tas, dengan mempertimbangkan berat dan nilai setiap barang.Ini contoh masalah Knapsack.
- Sudoku:Permainan puzzle ini juga termasuk masalah NP-Complete. Mencari solusi yang tepat untuk mengisi semua kotak dengan angka 1 sampai 9, dengan aturan tertentu, bisa jadi rumit banget, apalagi kalau kamu punya Sudoku yang super susah.
Mengapa Masalah NP-Complete Sulit Diselesaikan Secara Efisien?
Masalah NP-Complete sulit dipecahkan secara efisien karena kompleksitasnya yang tinggi. Untuk mencari solusi, komputer harus mengecek semua kemungkinan kombinasi, dan jumlah kemungkinan ini bisa tumbuh secara eksponensial seiring dengan meningkatnya ukuran masalah. Misalnya, untuk menyelesaikan masalah TSP dengan 10 kota, komputer harus mengecek 3.628.800 kemungkinan rute.
Tapi, kalau masalahnya ada 20 kota, jumlah kemungkinan rute yang harus dicek melonjak jadi 2.432.902.008.176.640.000! Itu banyak banget, lho! Nah, itulah mengapa masalah NP-Complete super sulit dipecahkan secara efisien. Sampai sekarang, belum ada cara yang pasti untuk menyelesaikan masalah ini dengan cepat dan mudah.
Analisis Kinerja Algoritma Genetika
Setelah memahami cara kerja Algoritma Genetika, langkah selanjutnya adalah menganalisis seberapa efektif algoritma ini dalam menyelesaikan masalah. Nah, dalam dunia pemrograman, kita punya banyak cara untuk menilai kinerja suatu algoritma. Untuk Algoritma Genetika, kita bisa menggunakan beberapa metrik yang khusus dirancang untuk mengukur performanya.
Metrik Penilaian Kinerja Algoritma Genetika
Metrik penilaian kinerja Algoritma Genetika memberikan gambaran tentang seberapa baik algoritma tersebut dalam menemukan solusi optimal atau mendekati optimal untuk suatu masalah. Berikut beberapa metrik yang sering digunakan:
- Akurasi: Menunjukkan seberapa dekat solusi yang ditemukan oleh Algoritma Genetika dengan solusi optimal sebenarnya. Akurasi diukur dengan membandingkan solusi yang dihasilkan dengan solusi optimal yang diketahui. Semakin tinggi akurasi, semakin baik algoritma dalam menemukan solusi yang mendekati optimal.
- Kecepatan Konvergensi: Menunjukkan seberapa cepat Algoritma Genetika dapat menemukan solusi yang optimal atau mendekati optimal. Kecepatan konvergensi diukur dengan menghitung jumlah generasi yang dibutuhkan untuk mencapai solusi yang diinginkan. Semakin cepat konvergensi, semakin efisien algoritma dalam menyelesaikan masalah.
- Ketahanan terhadap Noise: Menunjukkan seberapa baik Algoritma Genetika dalam mengatasi ketidakpastian atau noise dalam data atau parameter masalah. Ketahanan terhadap noise diukur dengan melihat seberapa besar pengaruh noise terhadap akurasi dan kecepatan konvergensi algoritma. Semakin tahan terhadap noise, semakin robust algoritma dalam menghadapi kondisi yang tidak ideal.
- Kompleksitas Komputasi: Menunjukkan seberapa banyak sumber daya komputasi yang dibutuhkan oleh Algoritma Genetika untuk menyelesaikan suatu masalah. Kompleksitas komputasi diukur dengan menghitung jumlah operasi yang dibutuhkan oleh algoritma untuk menyelesaikan masalah. Semakin rendah kompleksitas komputasi, semakin efisien algoritma dalam menggunakan sumber daya komputasi.
Penerapan Metrik dalam Masalah NP-Complete, Analisis Kinerja Algoritma Genetika pada Persoalan NP-Complete
Dalam konteks masalah NP-Complete, metrik kinerja Algoritma Genetika memiliki arti yang sangat penting. Masalah NP-Complete dikenal sebagai masalah yang sulit dipecahkan dalam waktu polinomial, artinya semakin besar ukuran masalah, semakin lama waktu yang dibutuhkan untuk menemukan solusi optimal. Algoritma Genetika, meskipun tidak menjamin solusi optimal dalam waktu polinomial, menawarkan cara untuk menemukan solusi yang mendekati optimal dengan efisiensi yang relatif baik.
Dalam kasus masalah NP-Complete, metrik seperti akurasi dan kecepatan konvergensi menjadi sangat relevan. Kita ingin mengetahui seberapa baik Algoritma Genetika dalam menemukan solusi yang mendekati optimal dalam waktu yang relatif singkat, mengingat keterbatasan waktu untuk menyelesaikan masalah NP-Complete.
Studi Kasus: Analisis Kinerja Algoritma Genetika pada Masalah Traveling Salesman
Masalah Traveling Salesman (TSP) adalah contoh klasik masalah NP-Complete. Dalam TSP, kita ingin menemukan rute terpendek yang mengunjungi semua kota dalam suatu set, dan kembali ke kota awal. Algoritma Genetika telah berhasil diterapkan untuk menyelesaikan masalah TSP. Dalam studi kasus ini, kita akan melihat bagaimana metrik kinerja Algoritma Genetika digunakan untuk menilai performanya dalam menyelesaikan masalah TSP.
Misalnya, dalam suatu studi kasus, Algoritma Genetika berhasil menemukan solusi yang mendekati optimal untuk TSP dengan akurasi 95% dalam 100 generasi. Ini menunjukkan bahwa Algoritma Genetika mampu menemukan solusi yang baik dengan kecepatan konvergensi yang relatif cepat. Selain itu, studi kasus ini juga menunjukkan bahwa Algoritma Genetika dapat mengatasi noise dalam data, seperti ketidakpastian dalam jarak antara kota-kota.
Perbandingan Kinerja Algoritma Genetika dengan Algoritma Lainnya
Algoritma Genetika bukan satu-satunya algoritma yang digunakan untuk menyelesaikan masalah NP-Complete. Ada banyak algoritma lain, seperti algoritma greedy, algoritma branch-and-bound, dan algoritma simulated annealing. Berikut tabel perbandingan kinerja Algoritma Genetika dengan algoritma lain dalam menyelesaikan masalah NP-Complete:
| Algoritma | Akurasi | Kecepatan Konvergensi | Kompleksitas Komputasi |
|---|---|---|---|
| Algoritma Genetika | Tinggi (mendekati optimal) | Relatif cepat | Relatif rendah |
| Algoritma Greedy | Rendah (mungkin tidak optimal) | Sangat cepat | Sangat rendah |
| Algoritma Branch-and-Bound | Tinggi (optimal) | Relatif lambat | Relatif tinggi |
| Algoritma Simulated Annealing | Tinggi (mendekati optimal) | Relatif lambat | Relatif tinggi |
Dari tabel di atas, kita dapat melihat bahwa Algoritma Genetika menawarkan keseimbangan yang baik antara akurasi, kecepatan konvergensi, dan kompleksitas komputasi. Algoritma Genetika mampu menemukan solusi yang mendekati optimal dengan kecepatan konvergensi yang relatif cepat dan kompleksitas komputasi yang relatif rendah.
Implementasi dan Evaluasi
Oke, jadi setelah kita membahas dasar-dasar Algoritma Genetika (AG) dan bagaimana ia bisa mengatasi masalah NP-Complete, saatnya kita menyelami bagaimana AG ini benar-benar dijalankan dan diuji.
Langkah-langkah Implementasi
Bayangkan AG sebagai seorang ahli puzzle yang mencoba menemukan solusi terbaik untuk masalah NP-Complete. Ahli puzzle ini punya beberapa langkah untuk menyelesaikannya:
- Representasi Kromosom:Pertama, kita harus mengodekan solusi masalah NP-Complete ke dalam bentuk yang dapat dipahami oleh AG. Ini seperti menerjemahkan puzzle ke dalam bahasa yang dipahami oleh ahli puzzle. Misalnya, untuk masalah Travelling Salesman, kromosom bisa berupa urutan kota yang harus dikunjungi.
- Inisialisasi Populasi:Selanjutnya, kita membuat populasi awal kromosom. Ini seperti ahli puzzle yang memulai dengan beberapa ide awal untuk menyelesaikan puzzle.
- Fungsi Kebugaran:Ini adalah kunci untuk menilai seberapa baik sebuah solusi. Fungsi kebugaran menentukan skor untuk setiap kromosom, semakin tinggi skornya, semakin baik solusinya. Misalnya, untuk masalah Travelling Salesman, fungsi kebugaran bisa menghitung total jarak yang ditempuh.
- Seleksi:AG memilih kromosom terbaik berdasarkan fungsi kebugaran. Bayangkan ahli puzzle memilih ide-ide terbaik yang memiliki potensi untuk menyelesaikan puzzle.
- Crossover:AG menggabungkan kromosom terbaik untuk menciptakan kromosom baru. Ini seperti ahli puzzle menggabungkan ide-ide terbaik untuk mendapatkan ide baru yang lebih baik.
- Mutasi:AG membuat perubahan acak pada kromosom. Ini seperti ahli puzzle mencoba pendekatan baru untuk menyelesaikan puzzle.
- Iterasi:Langkah-langkah seleksi, crossover, dan mutasi diulang berulang kali hingga ditemukan solusi yang memuaskan. Ini seperti ahli puzzle terus mencoba ide-ide baru hingga menemukan solusi terbaik.
Evaluasi Kinerja
Setelah AG diimplementasikan, kita perlu menilai seberapa baik ia menyelesaikan masalah NP-Complete. Ada beberapa cara untuk mengevaluasi kinerja AG:
- Kecepatan Konvergensi:Seberapa cepat AG menemukan solusi optimal? Ini seperti mengukur seberapa cepat ahli puzzle menemukan solusi puzzle.
- Kualitas Solusi:Seberapa baik solusi yang ditemukan oleh AG? Ini seperti menilai seberapa baik solusi puzzle yang ditemukan oleh ahli puzzle.
- Stabilitas:Seberapa konsisten kinerja AG dalam berbagai skenario? Ini seperti mengukur seberapa konsisten ahli puzzle menyelesaikan puzzle.
Contoh Kode Program
Berikut adalah contoh kode program sederhana AG untuk menyelesaikan masalah Travelling Salesman:
“`pythonimport random
def fitness(chromosome): # Hitung total jarak yang ditempuh total_distance = 0 for i in range(len(chromosome) – 1): total_distance += distance_matrix[chromosome[i]][chromosome[i + 1]] total_distance += distance_matrix[chromosome[-1]][chromosome[0]] return 1 / total_distance # Maksimalkan kebugaran
def crossover(parent1, parent2): # Crossover satu titik crossover_point = random.randint(1, len(parent1) – 1) child = parent1[:crossover_point] + parent2[crossover_point:] return child
def mutation(chromosome): # Mutasi swap index1 = random.randint(0, len(chromosome) – 1) index2 = random.randint(0, len(chromosome) – 1) chromosome[index1], chromosome[index2] = chromosome[index2], chromosome[index1] return chromosome
# Inisialisasi populasi population = [] for i in range(population_size): chromosome = list(range(num_cities)) random.shuffle(chromosome) population.append(chromosome)
# Loop utama for generation in range(num_generations): # Evaluasi kebugaran fitness_scores = [fitness(chromosome) for chromosome in population]
# Seleksi parents = selection(population, fitness_scores)
# Crossover dan Mutasi new_population = [] for i in range(population_size): parent1, parent2 = random.sample(parents, 2) child = crossover(parent1, parent2) child = mutation(child) new_population.append(child) population = new_population
# Temukan solusi terbaik best_chromosome = population[fitness_scores.index(max(fitness_scores))] print(“Solusi terbaik:”, best_chromosome) “`
Hasil Evaluasi
Hasil evaluasi menunjukkan bahwa AG mampu menemukan solusi yang cukup baik untuk masalah NP-Complete dalam waktu yang relatif singkat. Namun, kinerja AG sangat bergantung pada parameter-parameter yang digunakan, seperti ukuran populasi, probabilitas crossover, dan probabilitas mutasi. Oleh karena itu, pemilihan parameter yang tepat sangat penting untuk mencapai kinerja optimal.
Kesimpulan dan Rekomendasi: Analisis Kinerja Algoritma Genetika Pada Persoalan NP-Complete
Analisis kinerja Algoritma Genetika (AG) pada masalah NP-Complete telah menunjukkan beberapa poin penting. AG terbukti efektif dalam menemukan solusi yang baik untuk masalah kompleks, terutama ketika solusi optimal sulit ditemukan dalam waktu yang wajar. Namun, ada keterbatasan yang perlu dipertimbangkan.
Keterbatasan Algoritma Genetika
Meskipun AG memiliki potensi besar, ada beberapa keterbatasan yang perlu dipertimbangkan dalam menyelesaikan masalah NP-Complete. Beberapa keterbatasan utama meliputi:
- Kemungkinan Terjebak dalam Minimum Lokal:AG dapat terjebak dalam minimum lokal, yaitu solusi yang baik, tetapi bukan solusi optimal. Hal ini dapat terjadi ketika algoritma tidak mampu menemukan solusi yang lebih baik di sekitar titik minimum lokal yang telah ditemukan.
- Parameter Tuning:AG memiliki banyak parameter yang perlu disetel dengan cermat, seperti ukuran populasi, probabilitas crossover, dan probabilitas mutasi. Penyetelan parameter yang buruk dapat mengakibatkan kinerja algoritma yang buruk.
- Waktu Komputasi:Untuk masalah NP-Complete yang kompleks, AG mungkin memerlukan waktu komputasi yang lama untuk menemukan solusi yang baik. Hal ini dapat menjadi kendala dalam aplikasi praktis.
Rekomendasi untuk Penelitian Lebih Lanjut
Ada beberapa area penelitian yang menarik terkait AG dan masalah NP-Complete. Beberapa rekomendasi meliputi:
- Pengembangan Strategi Pencarian Baru:Penelitian lebih lanjut dapat difokuskan pada pengembangan strategi pencarian baru yang dapat membantu AG menghindari minimum lokal dan menemukan solusi optimal dengan lebih efisien.
- Optimasi Parameter:Penelitian dapat dilakukan untuk mengembangkan teknik otomatis atau semi-otomatis untuk mengoptimalkan parameter AG untuk berbagai masalah NP-Complete.
- Hibridisasi dengan Algoritma Lain:AG dapat dikombinasikan dengan algoritma lain, seperti Simulated Annealing atau Tabu Search, untuk meningkatkan kinerja dalam menyelesaikan masalah NP-Complete.
Simpulan Akhir

Nah, sekarang kamu udah tahu betapa kerennya Algoritma Genetika dalam menghadapi masalah NP-Complete! Meskipun ada beberapa keterbatasan, Algoritma Genetika tetap jadi senjata ampuh untuk menemukan solusi yang optimal untuk masalah-masalah super sulit. Dengan terus berkembangnya teknologi dan penelitian, Algoritma Genetika punya potensi besar untuk memecahkan masalah-masalah yang lebih kompleks di masa depan.
Jadi, siap-siap untuk berpetualang di dunia Algoritma Genetika dan NP-Complete, dan temukan solusi yang inovatif untuk masalah-masalah yang menantang!
Jawaban untuk Pertanyaan Umum
Apa contoh masalah NP-Complete yang sering dijumpai?
Contoh masalah NP-Complete yang sering dijumpai adalah Traveling Salesman Problem (TSP), yang bertujuan untuk menemukan rute terpendek yang mengunjungi semua kota dalam satu perjalanan. Masalah lain adalah Knapsack Problem, yang bertujuan untuk memilih barang-barang dengan nilai maksimal yang dapat dimasukkan ke dalam tas dengan kapasitas terbatas.
Bagaimana cara kerja Algoritma Genetika?
Algoritma Genetika bekerja dengan menciptakan populasi solusi awal yang kemudian diubah melalui proses seleksi, crossover, dan mutasi. Solusi terbaik akan dipilih dan direplikasi untuk menghasilkan generasi berikutnya, sehingga solusi yang lebih baik akan muncul seiring waktu.
Apakah Algoritma Genetika selalu memberikan solusi optimal?
Algoritma Genetika tidak selalu memberikan solusi optimal, tetapi memberikan solusi yang baik dalam waktu yang relatif singkat. Kinerja Algoritma Genetika tergantung pada berbagai faktor seperti ukuran populasi, operator genetika yang digunakan, dan parameter algoritma.